-
漏れ量の計算式の導出
1. 気体の状態方程式とボイル・シャルルの法則
気体の状態方程式は、気体の絶対圧力\((P)\)、体積\((V)\)、絶対温度\((T)\)、物質量\((n)\)、気体定数\((R)\)の関係を示す基本的な式であり、以下のように表されます。
\(\mathit{PV = nRT}\)
この式は、ボイルの法則とシャルルの法則を組み合わせたものであり、理想気体の挙動を記述する際に用いられます。
■ ボイルの法則 (Boyle’s Law)
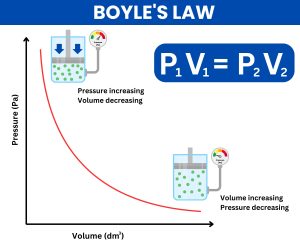
温度が一定のとき、気体の絶対圧力と体積は反比例します。
\(\displaystyle P_{1}\cdot V_{1} = P_{2}\cdot V_{2}\quad (T\text{ 一定})\)
\(P_{1}\) : 初期の絶対圧力
\(V_{1}\) : 初期の体積
\(P_{2}\) : 最終の絶対圧力
\(V_{2}\) : 最終の体積
\(T\) : 絶対温度
圧力が増加すれば体積が減少し、圧力が減少すれば体積が増加する関係です。
■ シャルルの法則(Charles’s Law)
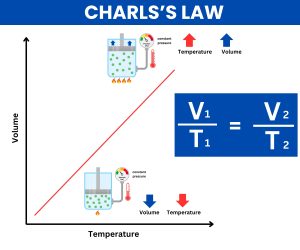
圧力が一定のとき、気体の体積は絶対温度に比例します。
\(\displaystyle \frac{V_{1}}{T_{1}} = \frac{V_{2}}{T_{2}}\quad (P\text{ 一定})\)
\(V_{1}\) : 初期の体積
\(T_{1}\) : 初期の絶対温度
\(V_{2}\) : 最終の体積
\(T_{2}\) : 最終の絶対温度
\(P\) : 圧力
温度が上昇すれば体積も増加し、温度が下降すれば体積が減少する関係です。
■ ボイル・シャルルの法則(Boyle Charles’ Law)
一定量の気体の体積は絶対圧力に反比例し、絶対温度に比例する。
\(\displaystyle \frac{P_{1}\cdot V_{1}}{T_{1}} = \frac{P_{2}\cdot V_{2}}{T_{2}}\)
\(P_{1}\) : 初期の絶対圧力
\(V_{1}\) : 初期の体積
\(T_{1}\) : 初期の絶対温度
\(P_{2}\) : 初期の絶対圧力
\(V_{2}\) : 最終の体積
\(T_{2}\) : 最終の絶対温度
2. エアリークテスターにおける漏れ量 \(Q\) (mL/min) の導出

エアリークテスターでは、密閉された容器内の圧力変化を測定することで、漏れ量を推定します。
温度が一定であると仮定し、漏れの前後にボイルの法則を適用します。
式1 \(\quad P_{1}\cdot V = P_{2}\cdot V + P_{0} \cdot \Delta V \quad (T\text{ 一定})\)
式2 \(\quad \Delta P = P_{1}-P_{2}\)
式1と式2を用いて、次の式を導出できます。
\(\displaystyle \Delta V = V \times \frac{(P_{1}-P_{2})}{P_{0}} = V \times \frac{\Delta P}{P_{0}} \quad (T\text{ 一定}) \)
\(P_{1}\) : 漏れる前の絶対圧力 (Pa)
\(P_{2}\) : 漏れた後の絶対圧力 (Pa)
\(P_{0}\) : 大気圧 (Pa)
\(\Delta P\) : 差圧 (Pa)
\(V\) : ワークの内容積 (mL)
\(T\) : 絶対温度
漏れ量の計算式では、「漏れ検出時間 \(t\) の間に、どれだけ圧力が下がったか \(\Delta P\)」を使って、漏れの量 \(Q\) を求めます。
「1秒あたりの漏れ量 \(Q\)」を求めるには、\(\Delta V\) を漏れ検出時間 \(t\) で割ります。
さらに、\(60\) を掛けることで、「1分あたりの漏れ量 \(Q\)」に換算できます。
\(\displaystyle Q = \Delta V \times \frac{60}{t} = V \times \frac{\Delta P}{P_{0}} \times \frac{60}{t} \quad (T\text{ 一定}) \)
\(Q\) : 漏れ量 (mL/min)
\(t\) : 漏れ検出時間 (s)
\(P_{0}\) に大気圧 (\(1.013\times 10^{5}\) ) を代入する。
\(\displaystyle Q = V \times \frac{\Delta P}{1.013\times 10^{5}} \times \frac{60}{t} \quad (T\text{ 一定}) \)
この式は、エアリークテスターにおける漏れ量の計算に広く使用されています。
漏れ量 \(Q\) (mL/min)計算ペーシへ